Table Of Content

In the popular form of active filter realizations, higher order forms are realized as cascades of second-order sections for even n, with the addition of a first order section if n is odd. The reason for this is that second-order sections are easy to design, adjust and debug, and lead to a standardized modular construction of higher order filters. The parameters of second-order sections have reasonably low sensitivity to component variations. Where n is the order of the filter and fc is the frequency at which the transfer function magnitude is reduced by 3 dB. This class of filters has a monotonically decreasing amplitude characteristic. It has no ripples in the passband, in contrast to Chebyshev and some other filters, and is consequently described as maximally flat.
Transition Band Width and Filter Order
The filter order refers to the number of reactive components, such as capacitors or inductors, used in the filter design. Higher-order filters can achieve steeper roll-off characteristics but may require more complex circuitry. Stopband attenuation refers to the amount of attenuation applied to frequencies outside the passband. It is important to ensure that unwanted frequencies are sufficiently attenuated to prevent interference. Passband ripple refers to the variation in gain within the passband of the filter. Minimizing passband ripple is crucial for maintaining signal integrity and avoiding distortions.
Filter Image
Because the sum of the angles is fixed, one can at most select the values of two of the specifications. The third specification will be determined by the particular design algorithm. Moreover, as with the angles in a triangle, if we make one of the specifications larger/smaller, it will impact one or both of the other specifications. Filters eliminate unwanted artifacts from signals to enhance their quality and prepare them for further processing. Digital filters are used in a variety of signal processing tasks including outlier and noise removal, waveform shaping, signal smoothing, and signal recovery.
Functions
Elliptic filters generalize Chebyshev and Butterworth filters by allowing for ripple in both the passband and the stopband. As ripples are made smaller, elliptic filters can approximate arbitrarily close the magnitude and phase response of either Chebyshev or Butterworth filters. The flatness in the passband and stopband causes the transition band to be very wide. The upper half of the GUI displays information on filter specifications and responses for the current filter. The Current Filter Information region, in the upper left, displays filter properties, namely the filter structure, order, number of sections used and whether the filter is stable or not.
High-Pass Filters: Shaping Signals from the Top
It is also sometimes called a Cauer filter or a rational Chebyshev filter, and it has equal ripple approximation error in both pass and stopbands. This means that any requirement on the filter's locality also implies a bound on its frequency function's width. Consequently, it may not be possible to simultaneously meet requirements on the locality of the filter's impulse response function as well as on its frequency function. Choosing the right components is crucial for achieving optimal filter performance. Factors such as component tolerances, temperature stability, and parasitic effects must be considered.
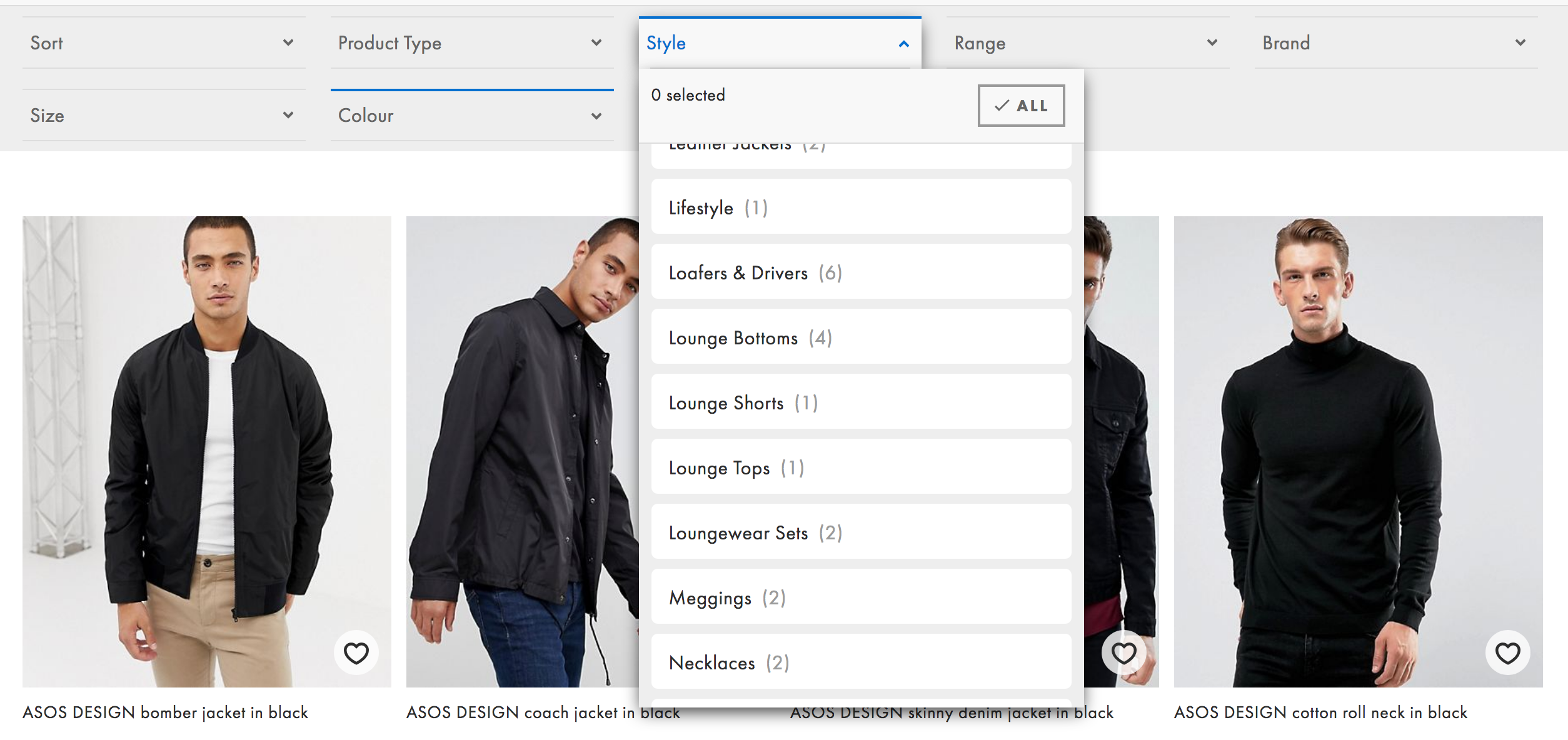
These sections often cause customers to scroll vertically, slowly, accurately, with extreme focus and precision. As they do so on mobile, some filters get activated by mistake, prompting the customer to be even more focused. A classic example of this pattern is the “Brands” filter, which often contains hundreds of options, sorted by popularity or by alphabet. Filters never exist on their own; in one way or another, they are always connected to the results that they are acting upon. This connection often causes filters and matching results to be somewhat synchronous, as the latter depend on how fast the UI registers an input, and how much time it needs to successfully process it.
Steeper roll-off characteristics result in better stopband attenuation but may introduce other design challenges. Minimum-order designs are obtained by specifying passband and stopband frequencies as well as a passband ripple and a stopband attenuation. The design algorithm then chooses the minimum filter length that complies with the specifications. This example shows how to design FIR and IIR filters based on frequency response specifications using the designfilt function in the Signal Processing Toolbox® product. The example concentrates on lowpass filters but most of the results apply to other response types as well. Microwave filters play an important role in any RF front end for the suppression of out of band signals.
Ansys partners with SynMatrix for faster RF filter design - Investing.com Canada
Ansys partners with SynMatrix for faster RF filter design.
Posted: Wed, 27 Mar 2024 07:00:00 GMT [source]
If you've been bummed you missed out on the dye-your-hair portion of quarantine, you'll be glad to know there's a major resurgence of the trend — and it's so easy. In fact, you don't have to dye your hair at all, because this new IG filter does all the work for you. As 2020 came to a close, a certain hair color filter started popping up all over Instagram Stories, and it has everyone trying out new hues with just a tap on the phone.
First Queen Elizabeth II Memorial Statue Unveiled, with a…
Digital filters offer advantages such as flexibility, easy reconfigurability, and the ability to implement complex algorithms. They are well-suited for applications where signal processing algorithms need to beoptimized, or where the filter characteristics need to be adjusted dynamically. Digital filters are commonly used in digital communication systems, image and audio processing, and biomedical signal analysis. Skirt selectivity refers to how sharply the filter attenuates frequencies outside the passband. Achieving high skirt selectivity is important for isolating the desired frequency band and rejecting unwanted frequencies. However, increasing skirt selectivity often comes at the cost of increased filter complexity and potential trade-offs in other performance parameters, such as passband ripple or phase response.

It is seen that Chebyshev filters have the advantage that a lower order polynomial will satisfy the specifications as compared to Butterworth filters. But on the other hand Butterworth filters have a more linear phase-characteristic than do Chebyshev filters, and this may affect the choice of design for specific cases. In the digital era, the choice between analog and digital filter implementation is not always crystal clear.
Once you have the perfect filter, you can do even more with the image before you export the finished product like adding text, frames, or animation. Table 1.2 will be used by the students to select the specifications of the filters to be built and tested for the duration of this laboratory. Each group will use the last four digits (designated M) of one social security number to determine the specifications of the filter which it needs to build. Comparing the above results to the original specification we find that the specifications are exceeded.
Analog filters offer advantages such as low latency, continuous signal processing, and precise control over filter parameters. They are well-suited for applications where real-time processing and high-fidelity signal reproduction are critical, such as audio systems or analog communication. The transition band width determines the range of frequencies over which the filter transitions from the passband to the stopband. A narrower transition band width allows for sharper roll-off characteristics but may introduce design challenges.
It’s also a good idea to compliment the filter with a search autocomplete and an alphabetical view if some of the popular options are highlighted at the top. A good example of it is Rozetka.ua, an eCommerce retailer from Ukraine (see above). An alternative option would be to show as many as 7–10 options at a time with an accordion that would expand and show all options on tap/click.

No comments:
Post a Comment